Contoh Soal PAS Matematika Wajib Kelas 10 Semester 1 2023/2024 ONLINE

Dalam rangka penyelenggaran Penilaian Akhir Semester di jenjang SMA, kami bermaksud membagikan Contoh Soal PAS Matematika Wajib Kelas 10 Semester 1 Tahun 2023/2024 ONLINE guna digunakan oleh siswa maupun guru semua jurusan.
Matematika wajib dikategorikan ke dalam mata pelajaran umum, tidak terikat oleh jurusan. Kami membuat latihan soal PAS Matematika Wajib dengan mengacu pada standar kurikulum 2013 revisi, dalam format daring dan offline, yang bisa dikerjakan/dipelajari menggunakan perangkat masing - masing.
Dokumen PDF yang berisikan rumus dan pemformatan lengkap kami sarankan untuk di download terlebih dahulu, setelah try out soal online. Karena sebagaimana yang kamu ketahui bahwa rumus matematika sangat tidak kompatible dengan platform website.
Selain itu, admin minta maat karena tidak adanya kunci jawaban dari naskah lampau pas SMA tahun kemarin tersebut.
Contoh Soal PAS Matematika Wajib Kelas 10 Semester 1 2023/2024 ONLINE
1. Jika a dan b berturut-turut adalah koefisien dari x2 dan x serta c adalah konstanta, maka nilai a, b dan c dari x2-8(x+1)=0 adalah ....
a. a=1,b=-8 dan c=8
b. a=1,b=8 dan c=-1
c. a=1,b=-8 dan c=-8
d. a=2,b=-8 dan c=-8
e. a=2,b=8 dan c=8
2. Akar akar persamaan kuadrat x2-7x+12=0 adalah adalah ....
a. –4 dan –3
b. –4 dan 3
c. –3 dan 4
d. 3 dan 4
e. 2 dan 5
3. Suatu persamaan kuadrat 3x2+5x-8=0 mempunyai akar-akar x1 dan x2. Nilai dari 5x1+5x2= ....
a. -40/3
b. -25/3
c. 25/3
d. 40/3
e. 50/3
4. Jika x1 dan x2 adalah akar-akar persamaan kuadrat 4x2+6x+8=0, nilai x1∙x2= ....
a. -2
b. -3/2
c. 1/2
d. 3/2
e. 2
5. Nilai diskriminan dari persamaan kuadrat 4x2+4x+1=0 adalah ....
a. -16
b. -1
c. 0
d. 16
e. 32
a. -2
b. -3/2
c. 1/2
d. 3/2
e. 2
5. Nilai diskriminan dari persamaan kuadrat 4x2+4x+1=0 adalah ....
a. -16
b. -1
c. 0
d. 16
e. 32
6. Berikut ini hubungan yang tepat antara nilai D dan jenis-jenis akar suatu persamaan kuadrat adalah ....
a. I dan III
b. II dan IV
c. I dan II
d. I dan IV
e. III dan IV
c. I dan II
d. I dan IV
e. III dan IV
Informasi berikut digunakan untuk mengerjakan soal nomor 7 dan 8.
Diberikan suatu fungsi kuadrat f(x)=x2-4x-12
7. Fungsi tersebut memotong sumbu X di ....
a. (-2,0) dan (-6,0)
b. (-2,0) dan (6,0)
c. (2,0) dan (-6,0)
d. (2,0) dan (6,0)
e. (0,-2) dan (0-6)
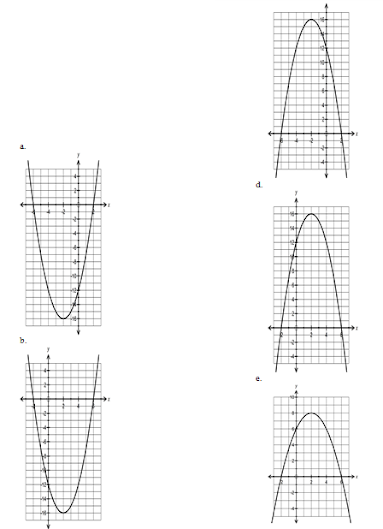
8. Gambar grafik yang tepat untuk fungsi tersebut adalah ....
Diberikan suatu fungsi kuadrat f(x)=x2-4x-12
7. Fungsi tersebut memotong sumbu X di ....
a. (-2,0) dan (-6,0)
b. (-2,0) dan (6,0)
c. (2,0) dan (-6,0)
d. (2,0) dan (6,0)
e. (0,-2) dan (0-6)
8. Gambar grafik yang tepat untuk fungsi tersebut adalah ....
9. Persamaan fungsi kuadrat dari parabola di bawah ini adalah ....
a. f(x)=x2-3x+4
b. f(x)=x2-4x-3
c. f(x)=x2-4x+3
d. f(x)=x2+4x-3
e. f(x)=x2+4x+3
10. Perhatikan grafik berikut !
Berikut ini informasi yang benar tentang fungsi di atas adalah ....
a. menyinggung sumbu X
b. parabola terbuka ke atas
c. memiliki titik balik maksimum
d. tidak memiliki sumbu simetri
e. memiliki asimtut
11. Perhatikan gambar berikut!
Ciri-ciri fungsi kuadrat dengan grafik seperti gambar di atas adalah ....
a. a < 0 dan D > 0
b. a < 0 dan D = 0
c. a > 0 dan D < 0
d. a > 0 dan D > 0
e. a > 0 dan D < 0
12. Agar grafik fungsi kuadrat f(x)=(p-4) x2+3x+5 terbuka ke atas, maka nilai p yang memenuhi adalah ....
a. p<4
b. p≤4
c. p=4
d. p≥4
e. p>4
13. Berikut ini yang menunjukkan grafik fungsi kuadrat adalah ....
a. p<4
b. p≤4
c. p=4
d. p≥4
e. p>4
13. Berikut ini yang menunjukkan grafik fungsi kuadrat adalah ....
14. Biaya pembuatan sebuah jaket berlogo adalah Rp. 200.000,-. Sedangkan biaya pengiriman untuk semua jaket berlogo yang dipesan adalah Rp. 100.000. Jika B(x) adalah total biaya pemesanan untuk x buah jaket, maka rumus total biaya pemesanan adalah ....
a. B(x)=300.000x
b. B(x)=200.000x+100.000
c. B(x)=100.000x+200.000
d. B(x)=200.000x-100.000
e. B(x)=300.000x-100.000
15. Perhatikan grafik fungsi 2x+4y=8 berikut !
Titik potong dengan sumbu Y dari grafik tersebut adalah ....
a. (0,2)
b. (0,3)
c. (0,4)
d. (2,0)
e. (4,0)
16. Diketahui f(x)=3x2+5 dan g(x)=2x-11. Hasil dari f(x)-g(x)= ....
a. 5x-6
b. 3x2-2x+6
c. 3x2-2x-6
d. 3x2+2x+16
e. 3x2-2x+16
17. Diketahui f(x)=x3+8x2+9x dan g(x)=-x3-5x2+x. Hasil dari (f+g)(x)= ....
a. -2x3+3x2+10x
b. 2x3+3x2+10x
c. 3x2+10x
d. 3x2-10x
e. 13x2+10x
18. Hasil perkalian f(x) dan g(x) dengan f(x)=x2+3x dan g(x)=x+2 yaitu ....
a. (f∙g)(x)=x3+3x2+6x
b. (f∙g)(x)=x3+2x2+6x
c. (f∙g)(x)=x3+5x2+6x
d. (f∙g)(x)=x3+5x2+6
e. (f∙g)(x)=x3+x2+6x
19. Gambar diagram panah yang menunjukkan fungsi komposisi yang benar adalah ....
20. Rumus komposisi fungsi (f∘g)(x) dengan f(x)=x2 dan g(x)=x+5 adalah ....
a. (f∘g)(x)=x2+5
b. (f∘g)(x)=x+25
c. (f∘g)(x)=x2+25
d. (f∘g)(x)=x2+10x
e. (f∘g)(x)=(x+5)2
a. (f∘g)(x)=x2+5
b. (f∘g)(x)=x+25
c. (f∘g)(x)=x2+25
d. (f∘g)(x)=x2+10x
e. (f∘g)(x)=(x+5)2
21. Diberikan f(x)=x3 dan g(x)=-1/x. Nilai komposisi fungsi (g∘f)(2) = ....
a. -1/8
b. -1/2
c. -1/4
d. 1/6
e. 1/8
22. Diketahui f(x)=2-x dan h(x)=3x+5. Rumus fungsi komposisi (f∘h)(x)= ....
a. 7-3x
b. 11-3x
c. -3-3x
d. 7+2x
e. 3+2x
23. Jika g(x)=√(x+5) dan h(x)=1/x2 , maka rumus fungsi (h∘g)(x)= ....
a. √(1/(x2+5))
b. √(1/x2 +5)
c. 1/√x+5
d. 1/x+5
e. 1/(x+5)
24. Jika f(x)=2x, g(x)=x3 dan h(x)=5+x, maka rumus fungsi (h∘f∘g)(x)= ....
a. 5+8x3
b. 5+2x3
c. 10+2x3
d. (10+2x)3
e. (5+2x)3
25. Diketahui (g∘f)(x)=5x+1 dan g(x)=4x maka rumus fungsi f(x)= ....
a. (5x+1)/4
b. 5x/4+1
c. 5x+1/4
d. 5x-3
e. (4x-1)/5
26. Jika (g∘h)(x)=x2+2 dan g(x)=3+x, maka rumus fungsi h(x)= ….
a. x2-1
b. x2+1
c. x2+5
d. (x2+2)/3
e. x2/3+2
27. Diketahui (g∘f)(x)=3x+2 dan f(x)=6x. Rumus fungsi dari g(x) = ....
a. x/2+4
b. x/2+1/3
c. x/2+2
d. 3x-4
e. 3x+4
28. Jika (f∘g)(x)=4x-5 dan g(x)=2x-3, maka f(x)= ....
a. 2x+11
b. 2x+6
c. 2x-1
d. 2x+1
e. 2x-11
29. Jika f(x)=3x, maka f(-1) (x)= ....
a. x+3
b. x-3
c. x/3
d. x3
e. ∛x
30. Jika g(x)=(x+3)/(2x-5), x≠5/2, maka invers fungsi g(x) adalah ....
a. g(-1) (x)=(x-3)/(2x+5), x≠-5/2
b. g(-1) (x)=(x-5)/(2x-3), x≠3/2
c. g(-1) (x)=(5x+3)/(2x-1), x≠1/2
d. g(-1) (x)=(5x-3)/(2x+1), x≠-1/2
e. g(-1) (x)=(5x-3)/(2x-1), x≠1/2
31. Jika f(x)=5/x maka nilai f(-1) (10) = ....
a. 1/2
b. 2
c. 5
d. 25
e. 50
32. Diketahui f(-1) (x)=(3-x)/7, maka rumus fungsi f(x)= ....
a. 3-7x
b. 3+7x
c. 7-3x
d. 7+3x
e. 3x-7
33. Sifat komposisi fungsi invers yang benar yaitu ....
a. (f(-1)∘g(-1) )(x)=(f∘g)(x)
b. (g(-1)∘f(-1) )(x)=(g∘f)(x)
c. (f(-1)∘g(-1) )(x)=(f∘g)(-1) (x)
d. (g(-1)∘f(-1) )(x)=(g∘f)(-1) (x)
e. (g(-1)∘f(-1) )(x)=(f∘g)(-1) (x)
34. Diketahui f(x)=6+2x, g(x)=5x+2, invers dari (g∘f) (x) adalah ....
a. (g∘f)(-1) (x)=(x+32)/10
b. (g∘f)(-1) (x)=(x-32)/10
c. (g∘f)(-1) (x)=10/(x-32),x≠32
d. (g∘f)(-1) (x)=10/(x+32),x≠-32
e. (g∘f)(-1) (x)=(32-x)/10
35. Jika f(-1) (x)=2x-4 dan g(-1) (x)=(1+x)/(x-5),x≠1/3, maka (g(-1)∘f(-1) )(x)= ....
a. (2x-3)/(2x-1),x≠1/2
b. (2x-3)/(2x+9),x≠-9/2
c. (2x-3)/(2x-9),x≠9/2
d. (2x+3)/(2x-9),x≠9/2
e. (2x-5)/(2x-9),x≠9/2
36. Diketahui (f∘g)(-1) (x)=(x-4)/3, dan f(x)=x-7, maka rumus fungsi g(x)= ....
a. 4x-3
b. 4x-11
c. 3x-3
d. 3x-11
e. 3x+11
37. Diketahui (g∘f)(-1) (x)=x2 , dan g(-1) (x)=3x, maka rumus fungsi f(-1) (x)= ....
a. x2/9
b. x2/3
c. x2+3
d. 3x2
e. 9x2
Bacaan berikut ini sebagai informasi untuk mengerjakan soal no 38-40.
Suatu industri rumah tangga di daerah X, para ibu dan kaum wanitanya bekerja dengan memintal benang dari kapas. Benang yang sudah jadi akan diproduksi lagi menjadi kain lokal oleh kelompok wanita yang lain. Semua proses tersebut dikerjakan secara swadaya oleh warga. Sehingga kampung ini sering mendapat penghargaan dari Bupati dikarenakan industri kain lokalnya.
Untuk membuat kapas menjadi benang, diperlukan beberapa kg kapas. Setiap 10 kg kapas bisa menghasilkan 5 kg benang dalam bentuk gulungan besar. Dan dari 5 kg benang bisa menjadi 2 kg kain yang berbentuk lembaran.
Kain yang sudah jadi, dikemas sedemikian rupa sehingga menjadi suvenir khas daerah tersebut.
38. Dari ilustrasi di atas, diagram yang tepat untuk menggambarkan rangkaian proses pembuatan kain yaitu ....
a. -1/8
b. -1/2
c. -1/4
d. 1/6
e. 1/8
22. Diketahui f(x)=2-x dan h(x)=3x+5. Rumus fungsi komposisi (f∘h)(x)= ....
a. 7-3x
b. 11-3x
c. -3-3x
d. 7+2x
e. 3+2x
23. Jika g(x)=√(x+5) dan h(x)=1/x2 , maka rumus fungsi (h∘g)(x)= ....
a. √(1/(x2+5))
b. √(1/x2 +5)
c. 1/√x+5
d. 1/x+5
e. 1/(x+5)
24. Jika f(x)=2x, g(x)=x3 dan h(x)=5+x, maka rumus fungsi (h∘f∘g)(x)= ....
a. 5+8x3
b. 5+2x3
c. 10+2x3
d. (10+2x)3
e. (5+2x)3
25. Diketahui (g∘f)(x)=5x+1 dan g(x)=4x maka rumus fungsi f(x)= ....
a. (5x+1)/4
b. 5x/4+1
c. 5x+1/4
d. 5x-3
e. (4x-1)/5
26. Jika (g∘h)(x)=x2+2 dan g(x)=3+x, maka rumus fungsi h(x)= ….
a. x2-1
b. x2+1
c. x2+5
d. (x2+2)/3
e. x2/3+2
27. Diketahui (g∘f)(x)=3x+2 dan f(x)=6x. Rumus fungsi dari g(x) = ....
a. x/2+4
b. x/2+1/3
c. x/2+2
d. 3x-4
e. 3x+4
28. Jika (f∘g)(x)=4x-5 dan g(x)=2x-3, maka f(x)= ....
a. 2x+11
b. 2x+6
c. 2x-1
d. 2x+1
e. 2x-11
29. Jika f(x)=3x, maka f(-1) (x)= ....
a. x+3
b. x-3
c. x/3
d. x3
e. ∛x
30. Jika g(x)=(x+3)/(2x-5), x≠5/2, maka invers fungsi g(x) adalah ....
a. g(-1) (x)=(x-3)/(2x+5), x≠-5/2
b. g(-1) (x)=(x-5)/(2x-3), x≠3/2
c. g(-1) (x)=(5x+3)/(2x-1), x≠1/2
d. g(-1) (x)=(5x-3)/(2x+1), x≠-1/2
e. g(-1) (x)=(5x-3)/(2x-1), x≠1/2
31. Jika f(x)=5/x maka nilai f(-1) (10) = ....
a. 1/2
b. 2
c. 5
d. 25
e. 50
32. Diketahui f(-1) (x)=(3-x)/7, maka rumus fungsi f(x)= ....
a. 3-7x
b. 3+7x
c. 7-3x
d. 7+3x
e. 3x-7
33. Sifat komposisi fungsi invers yang benar yaitu ....
a. (f(-1)∘g(-1) )(x)=(f∘g)(x)
b. (g(-1)∘f(-1) )(x)=(g∘f)(x)
c. (f(-1)∘g(-1) )(x)=(f∘g)(-1) (x)
d. (g(-1)∘f(-1) )(x)=(g∘f)(-1) (x)
e. (g(-1)∘f(-1) )(x)=(f∘g)(-1) (x)
34. Diketahui f(x)=6+2x, g(x)=5x+2, invers dari (g∘f) (x) adalah ....
a. (g∘f)(-1) (x)=(x+32)/10
b. (g∘f)(-1) (x)=(x-32)/10
c. (g∘f)(-1) (x)=10/(x-32),x≠32
d. (g∘f)(-1) (x)=10/(x+32),x≠-32
e. (g∘f)(-1) (x)=(32-x)/10
35. Jika f(-1) (x)=2x-4 dan g(-1) (x)=(1+x)/(x-5),x≠1/3, maka (g(-1)∘f(-1) )(x)= ....
a. (2x-3)/(2x-1),x≠1/2
b. (2x-3)/(2x+9),x≠-9/2
c. (2x-3)/(2x-9),x≠9/2
d. (2x+3)/(2x-9),x≠9/2
e. (2x-5)/(2x-9),x≠9/2
36. Diketahui (f∘g)(-1) (x)=(x-4)/3, dan f(x)=x-7, maka rumus fungsi g(x)= ....
a. 4x-3
b. 4x-11
c. 3x-3
d. 3x-11
e. 3x+11
37. Diketahui (g∘f)(-1) (x)=x2 , dan g(-1) (x)=3x, maka rumus fungsi f(-1) (x)= ....
a. x2/9
b. x2/3
c. x2+3
d. 3x2
e. 9x2
Bacaan berikut ini sebagai informasi untuk mengerjakan soal no 38-40.
Suatu industri rumah tangga di daerah X, para ibu dan kaum wanitanya bekerja dengan memintal benang dari kapas. Benang yang sudah jadi akan diproduksi lagi menjadi kain lokal oleh kelompok wanita yang lain. Semua proses tersebut dikerjakan secara swadaya oleh warga. Sehingga kampung ini sering mendapat penghargaan dari Bupati dikarenakan industri kain lokalnya.
Untuk membuat kapas menjadi benang, diperlukan beberapa kg kapas. Setiap 10 kg kapas bisa menghasilkan 5 kg benang dalam bentuk gulungan besar. Dan dari 5 kg benang bisa menjadi 2 kg kain yang berbentuk lembaran.
Kain yang sudah jadi, dikemas sedemikian rupa sehingga menjadi suvenir khas daerah tersebut.
38. Dari ilustrasi di atas, diagram yang tepat untuk menggambarkan rangkaian proses pembuatan kain yaitu ....
39. Misalkan f(k) menyatakan kemampuan produksi dari mesin pertama dan k adalah banyaknya bahan baku kapas dalam kg. Dari bacaan di atas, rumus f(k) dapat dituliskan dengan ....
a. f(k)=1/2 k
b. f(k)=2k
c. f(k)=5k
d. f(k)=7k
e. f(k)=10k
40. Mesin ke II dapat memproses 5 kg benang menjadi 2 kg kain. Misalkan g(b) menyatakan kemampuan produksi dari mesin II, rumus g(b)=2/5 b dengan b adalah banyaknya benang dalam kg. Pernyataan tentang komposisi fungsi dari f dan g dinyatakan dengan ....
a. (g∘f)(k)=g(f(k))=1/5 k
b. (g∘f)(k)=g(f(k))=1/2 k
c. (g∘f)(k)=g(f(k))=2k
d. (g∘f)(k)=g(f(k))=5k
e. (g∘f)(k)=g(f(k))=10k
Dokumen PDF : DOWNLOAD